Simmetria e simmetrizzazione nella struttura Maxwelliana delle equazioni, Il problema della spaziotemporalità in Einstein e l'inconciliabilità fra relatività e meccanica quantistica. Altre questioni inerenti alla percezione simmetrica del realeProf. Roberto Ettore BertagnolioHeisemberg una volta affermò: "La radice ultima dei fenomeni non è la materia, ma la legge matematica, la simmetria, la forma matematica". Il mio intento, il mio compito principale nella vita è dimostrare che quest'affermazione è una stupidaggine. Il concetto di Simmetria non è una base di partenza (Galois) ma un punto di arrivo frutto dell'anomalia originaria. Se lo si scambia come base, si rischia di costruire un'impalcatura gigantesca sulle sabbie mobili. La teoria dei gruppi è alla base di questo fraintendimento, essa parte da questa base per costruire tutto l'edificio matematico, parte cioè dall'anomalia percettiva che si presenta "come proiezione di una realtà simmetrica naturale". La simmetria non è un dato naturale ma una anomalia percettiva profonda, che ha le sue basi nello scarto fra s. specifico e non, che va oltre il segno matematico e raggiunge il simbolico. (rif. schema base sul pensiero logico -simbolico)
 Questo del simbolico, è un limite congenito della struttura matematica, che coincide col limite percettivo. Il passaggio successivo è la simmetria, quest'ultima è un filtro con il quale guardiamo l'Universo. Diventa la percezione anomala tridimensionale, come risultato del simmetrico naturalizzato come reale.
COMPRENDENDO IL SIGNIFICATO DELLA PROFONDITÀ STRUTTURALE, SI EVITA LA SIMMETRIZZAZIONE DELLE EQUAZIONI, ANCHE SE APPAIONO PALESEMENTE ASIMMETRICHE*. LA SIMMETRIZZAZIONE DELLA STRUTTURA MATEMATICA NON AVVIENE A LIVELLO SEMIOTICO MA AD UN LIVELLO PIł PROFONDO. *EQUAZIONE DI MAXWELL NELLA LORO FORMA BASE INTEGRALE ASIMMETRICA.

Anche nel caso delle equazioni di Maxwell, l'asimmetria delle equazioni ha origine nella traslazione dal simbolo al segno. Matematicamente vuol dire riscrivere le equazioni considerando LO SPAZIO VUOTO dove non siano presenti né correnti (ì=0) né cariche elettriche (q=0), così otteniamo le equazioni completamente SIMMETRICHE. In questo caso, se consideriamo lo SPAZIO VUOTO, questa visione dello SPAZIO è coerente con L'ANOMALIA ORIGINARIA e nello stesso tempo con la struttura SIMMETRICO-SIMBOLICA. IL PRIMO PASSO LOGICO é LA NON ASSUNZIONE DEL CONCETTO "SIMMETRICO" COME BASE DI PARTENZA DELLA STRUTTURA MATEMATICA EVITANDO LA COINCIDENZA DI QUEST'ULTIMA CON LA "REALT "FISICO-TEORICA" E CON LA REALTÀ "NATURALE". DA QUESTO PUNTO DI VISTA IL PROBLEMA DELLA "ROTTURA" SPONTANEA DELLA SIMMETRIA E' UN FALSO PROBLEMA*: IL VERO PROBLEMA RIMANE LA DISFUNZIONE PERCETTIVA CONGENITA, CHE SI CONCRETIZZA ATTRAVERSO LA CATEGORIA "TRASCENDENTALE" DEL SIMMETRICO (Per dirla con il Kant della Ragion pura).
*Sono sempre più convinto che il problema della "rottura" tale fenomeno legato alla fisica delle particelle la stessa deviazione interpretativa, la stessa devianza alla quale è incorso Einstein nell'interpretare nell'analizzare del 19 sulla "curvatura dello spazio", derivante sempre dalla disfunzione percettiva fra i due sistemi (rif.schema). Le particelle in questione hanno una massa gravitazionale. é vero che la loro massa è irrilevante, ma io credo che, seppur la forza gravitazionale sia la forza più debole in natura, essa interagisca fra i due sistemi. In qualche modo i fisici , dovranno spiegare al mondo perché la SIMMETRIA viene conservata per distanze brevi (energia alta) ma "SCOMPARE"** SENZA FORZATURA ad energia bassa per distanze elevate. **(mi sembra più adeguato l'azione dello "scomparire"piuttosto che rompersi).

Possiamo a questo punto stabilire una prima legge: IL SIMMETRICO HA BISOGNO DI UNO SPAZIO FINITO é QUINDI NEL VUOTO CHE SI CONCRETIZZA PERCETTIVAMENTE L'ANOMALIA TRIDIMENSIONALE. LO SPAZIO VUOTO é IMPLICITO AL SIMMETRICO, PER QUESTO L0 SPAZIO QUANTISTICO NON PUń ESSERE TALE. SOLTANTO SUPERANDO QUESTO LIMITE COGNITIVO, POSSIAMO COSTRUIRE UNO SPAZIO QUANTISTICO, CHE NON PUń ESSERE SIMMETRICO. SE CONTINUIAMO AD INTERPRETARLO COME SIMMETRICO, ALLORA RIUSCIAMO AD UNIFICARE LE DUE TEORIE , MA AD UNA CONDIZIONE:CHE NOI "RELATIVIVIZZIAMO" LA MECCANICA QUANTISTICA(4).
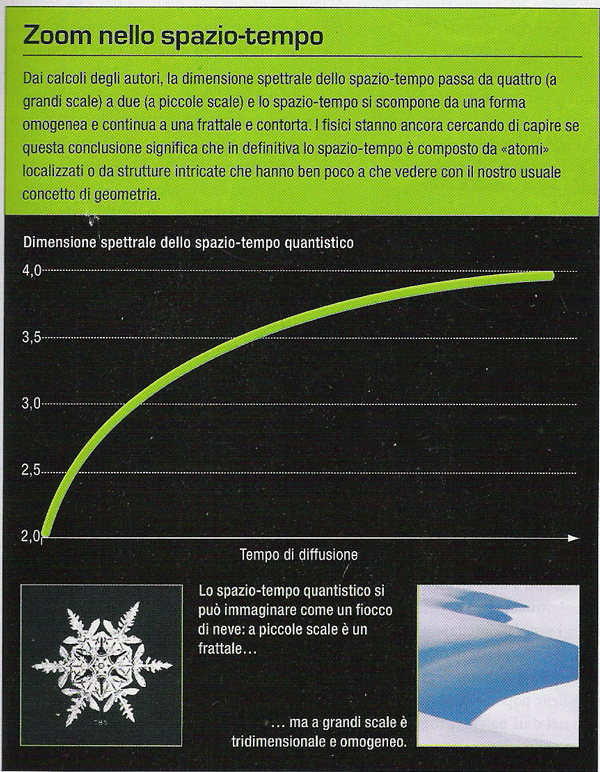 (Le Scienze settembre 2008)
SIMMETRIA, FISICA E LEGGI DELLA NATURA. LA QUESTIONE DELLA SIMMETRIA SPAZIOTEMPORALE IN EINSTEIN E IL RIBALTAMENTO DELLA LOGICA DI BASE.
Non è dagli esperimenti che possono essere dedotte le leggi di simmetria ma è da quest'ultima che possono essere dedotte le leggi nella loro universalità. Einstein ribadisce questa convinzione che possiamo definirla NON FENOMENOLOGICA, che non parte cioè dall'esperienza per ribadire un principio, ma dal principio stesso, e quest'ultimo è visto come un filtro rigido, come una categoria "trascendentale", partendo dal presupposto che le leggi devono essere dedotte dal PRINCIPIO DI SIMMETRIA. Questo rovesciamento della logica dell'interpretazione fisica dell'universo, l'adattamento di esso alla struttura matematica di base, parte anch'essa (Galois) da una struttura simmetrica, l'accordo della fisica teorica con la struttura matematica, Einstein lo trova innanzitutto nella simmetria tra l'osservatore(sogg.) e la velocità costante della luce(ogg.)". La velocità della luce è esattamente la stessa per tutti gli osservatori". La indubitabile costanza della velocità della luce, da una mano ad Einstein per eludere i limiti strutturali della percezione , lo scarto percettivo fra soggetto-oggetto. La luce viaggia sempre in uno spazio 3D, ma unendo indissolubilmente SPAZIO-TEMPO si ottiene la quadridimensionalità proposta da Einstein nel contesto della Relatività ristretta per salvare il concetto di SIMMETRIA (il suo caro Dio non si abbasserà mai a giocare i dadi col mondo) e si illude di correggere L'ANOMALIA con L'ANOMALIA, OVVERO IL QUADRIDIMENSIONALE che ha come conseguenza inevitabile LA CURVATURA DELLO SPAZIO . In realtà quello che non può risolvere matematicamente è L'ANOMALIA TRIDIMENSIONALE, non la può risolvere con LA STRUTTURA MATEMATICA perché tale struttura è già frutto di tale anomalia. Einstein non può abbandonare il simmetrico e qui si spiega |