Note sull'inibizione matematicadi Jorge Canestri e Silva Oliva(Questo articolo è stato pubblicato nel numero 70 della rivista: Il piccolo Hans).A) PREMESSA Il campionario delle reazioni spontanee delle persone, anche colte, che si trovano di fronte alla necessità di comprendere o eseguire delle operazioni mentali che sono di natura astratta e richiedono l'uso di formalismi matematici, è alla portata di chiunque e non richiede illustrazione. Si può forse osservare una maggior consapevolezza, nella cultura odierna, circa la enormità di questo deficit e circa le conseguenze che esso comporta. Come autori di queste note, nelle vesti alternative e successive, nelle nostre vite di matematici, insegnanti e psicoanalisti, abbiamo voluto affrontare l'argomento adoperando esempi tratti da campi diversi: alcuni di essi provengono dall'insegnamento, altri dalla pratica clinica. Si tratta comunque di difficoltà comuni a tanti soggetti, che si rivelano in modo appariscente in età scolastica, per due motivi. Il primo dipende certamente dal precipuo momento dello sviluppo delle strutture cognitive. Il secondo dal banale fatto che queste strutture vengono a contatto con la materia in questione. La matematica che s'impara nella scuola elementare, nella misura in cui richiede l'apprendimento di un numero basso di simboli, l'apprendimento, necessariamente meccanico, degli algoritmi delle operazioni razionali e il riconoscimento di alcune forme geometriche elementari, ha un indice di difficoltà inferiore alla lettura di testi (DSM III R). Le difficoltà alle quali facciamo riferimento sono dunque quelle relative agli argomenti insegnati nelle scuole medie e superiori. Restano esclusi, ovviamente, quei soggetti che per mestiere, o per diletto, hanno familiarità con la matematica e sono andati oltre il livello medio d'insegnamento scolastico. L'esperienza quotidiana e professionale ci insegna che queste difficoltà sono comuni, come dicevamo dinanzi, tra la popolazione adulta, che ha già superato la scuola. La differenza tra questa e la popolazione scolastica risiede nel fatto che quest'ultima non può, a differenza della prima, sottrarsi alle esigenze di imparare e di adoperare nozioni matematiche. La stessa esperienza ci suggerisce, inoltre, che la modalità essenziale con la quale il soggetto affronta il mondo dell'astrazione matematica è, per l'appunto, quella del sottrarsi al confronto. Vedremo in seguito quali nomi, quali caratteristiche e quali motivazioni potrebbero corrispondere a questo generico moto di sottrazione che qui ipotizziamo. Nel rivedere la letteratura psicoanalitica abbiamo notato (senza avanzare nessuna pretesa di essere stati esaurienti), che l'argomento, così come lo proponiamo, non è stato specificamente preso in considerazione. Ci sono invece diversi lavori che si sono occupati del "talento" matematico e dello sviluppo, la genesi e la metapsicologia del pensiero astratto (V.H. Rosen, 1953), dello specifico narcisismo del matematico (R. Fine e B. Fine, 1977), delle relazioni tra matematica e inconscio e pre-conscio (S. Ferenczi, J. Lacan, I. Matte Blanco), ecc. Il campo che delimitiamo quindi, è molto più ristretto, si tratta infatti di interrogare gli ostacoli che si presentano ai soggetti messi a confronto con la matematica che si impara a scuola, e che possono manifestarsi sia nel periodo scolastico che successivamente nella vita. I soggetti da noi considerati non sono matematici né individui particolarmente dotati in tal senso, ma non sono neppure affetti da ritardi mentali o da difetti evidenti. E' una popolazione numerosa, è una difficoltà diffusa. Il matematico americano John Allen Paulos (1988) creò il neologismo "innumeracy" (di difficile traduzione), per designare l'analfabetismo matematico, e scrisse il libro: Innumeracy. Mathematical illiteracy and its consequences ai fini di analizzare gli effetti devastanti che esso comporta sul pensiero. Douglas Hofstadter la considera una grave malattia e l'autrice di un altro libro sullo stesso argomento - Sheila Tobias- ne parla in termini di "angoscia matematica". Il già citato Paulos annovera tra le cause di questo analfabetismo matematico, che si accompagna a rifiuto ed angoscia, una povera e sbagliata educazione scolastica, blocchi psicologici (psychological blocks ) e fraintendimenti romantici circa la natura stessa della matematica. Le nostre note sono incentrate su quelli che Paulos chiama "blocchi psicologici", essenzialmente per tre ordini di motivi. Il primo è ovvio, giacché il nostro è un tentativo di riflessione psicoanalitica sul problema; il secondo è che, pur non misconoscendo i difetti dell'educazione impartita nelle nostre (e altrui) scuole, la nostra esperienza ci insegna che, anche migliorando la qualità intrinseca dell'insegnamento ed aumentando la disponibilità e gli sforzi degli insegnanti, il problema, anche se si attenua, non scompare. Il terzo è che Paulos (ma come lui sembrano pensarla altri matematici) giudica paradossalmente "naturali" questi blocchi, apparentemente senza domandarsi quale è la ragione che li giustifica. Egli scrive infatti: "... alcuni dei blocchi per rapportarsi agevolmente con i numeri e le probabilità sono dovuti a risposte psicologiche completamente naturali all'incertezza, alla coincidenza o a come è inquadrato un problema. Altri possono essere attribuiti all'ansietà". Il quesito che si delinea è dunque quello di capire perché la matematica, che ha caratteristiche specifiche come forma di pensiero, può generare nel soggetto angoscia, blocchi psicologici e sforzi per sottrarsi alla sua pratica. Nella Premessa al suo bel libro Capire una dimostrazione , Gabriele Lolli (1988) dice che: "Definire la matematica è difficile, ci si sono provati inutilmente tutti i filosofi, mentre al matematico la definizione appare superflua; non ne ha bisogno per fare il suo lavoro". Non avrebbe quindi senso che ci si provassero anche gli autori di questo saggio e tuttavia, poiché il lettore non è un matematico al lavoro, è necessario enucleare almeno alcune di quelle caratteristiche che si rivelano fondamentali nel provocare delle risposte psicologiche. L'astrazione, nella sua espressione più compiuta, è sicuramente una caratteristica universalmente riconosciuta del pensiero matematico. Non si potrebbe però misconoscere che molte altre discipline raggiungono elevati livelli di astrazione. Ma la matematica associa a questa astrazione un discorso che "si articola come se parlasse di una realtà distinta da quella fisica, ma altrettanto oggettiva" (Lolli, op. cit., p. 192), una realtà che non ha alcuna corrispondenza diretta col mondo sensibile. Lo stesso autore ci ricorda il progetto leibniziano: "la mente sarà liberata dal dover pensare direttamente alle cose in se stesse, e tuttavia tutto verrà fuori correttamente". A ciò dobbiamo aggiungere un linguaggio assolutamente spoglio di valori semantici, un linguaggio che si risolve nella buona qualità della sintassi che lo informa. Questo formalismo è d'altronde distintivo dell'orientamento moderno della disciplina e della sua alleanza con la logica. Forse già in queste poche righe descrittive si possono intuire alcuni dei motivi che potrebbero essere all'origine dei disagi sperimentati da alcuni soggetti. In primo luogo si può percepire che il distacco dalla realtà fisica, sensibile, che fu sempre condizione sostanziale del pensiero matematico - basti pensare al precetto pascaliano "sostituire sempre mentalmente la definizione alla cosa definita", precetto d'altronde già presente in Aristotele, si è accentuato nella matematica dell'ultimo secolo. La storia della matematica (si veda a titolo illustrativo Eléments d'histoire des mathématiques di Nicolas Bourbaki, 1969) mette in evidenza questa progressiva e consistente alleanza tra metodo assiomatico, formalismo linguistico e logica nella matematica contemporanea. E' d'altronde noto che il pensiero in gestazione del matematico (non dell'utente comune), non ubbidisce linearmente a questi precetti metodologici generali che acquistano invece tutta la loro preminenza in sede di dimostrazione e di comunicazione. Tali precetti arrivano invece all'utente, seppure in versioni che di volta in volta vengono adeguate ai livelli di apprendimento. I resoconti, più o meno romanzati, dell'attività creativa di molti matematici (da Poincaré a Kac o a Hardy) offrono un dilettevole e utile materiale dimostrativo di questa asserzione. In secondo luogo è abbastanza evidente, anche se scarsamente riconosciuto, il divorzio tra matematica e psicologia. Fanno infatti eccezione quei matematici o quei logici che si sono interrogati circa il rapporto esistente tra i metodi di pensiero in sede di dimostrazione o validazione matematico-logica e i processi di pensiero dell'uomo comune alle prese con la soluzione di un problema. L'aspetto forse più interessante e valido della ricerca di Philip Johnson-Laird nel campo della psicologia cognitiva (cfr. Mental Models, 1983) è, per l'appunto, la dimostrazione della differenza di procedura tra il pensiero comune (problem solving ) e quello logico-matematico. Tra le eccezioni di cui sopra va menzionato il già citato Lolli, che affronta specificamente il problema nel suo libro sulla dimostrazione, ipotizzando che un errore a livello di concezione psicologica possa avere delle conseguenze negative a livello teorico o didattico. Noi condividiamo questa ipotesi e indirettamente desidereremmo che queste note, oltre a centrare l'obiettivo principale di fare un po' di luce sulle ragioni dell'"angoscia matematica", contribuissero in qualche misura a lottare contro l'analfabetismo matematico.
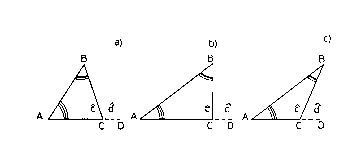
B) CARATTERISTICHE DELLA MATEMATICA Come va che la matematica, essendo fondamentalmente (Albert Einstein, 1920) Si può iniziare a parlare di matematica quando si abbandona il semplice contare per ricercare un metodo abbreviato per ottenere il risultato di cui si richiede una dimostrazione di "correttezza": "... la dimostrazione segna in genere il passaggio alla matematica vera e propria da una fase propedeutica di acquisizione di abilità e nozioni che si dicono matematiche ma che sono solo un prolungamento della padronanza fisica dell'ambiente esterno, e che servono a un controllo più efficiente dello stesso" (Lolli, p. 9). Per questo le difficoltà alle quali ci riferiamo sono relative agli argomenti insegnati nelle scuole medie inferiori e superiori. Al di là dei livelli elementari, infatti, si manifestano specifiche difficoltà insite nel fatto che la matematica diventa un linguaggio autonomo, che conserva dei legami con quello naturale ma si pone come un linguaggio artificiale, il cui apprendimento non è sostenuto né motivato dalla pratica quotidiana della comunicazione immediata. Si configura come una sorta di "lingua morta", nella quale i termini hanno un significato indipendente dal senso usuale delle parole che pronunciamo e che scaturisce da giustificazioni che risultano oscure nell'immediato. Per questo in un primo momento il linguaggio matematico si pone come una necessità imposta autoritariamente. Questo carattere "dogmatico" del linguaggio matematico viene spesso considerato con avversione e suscita l'accusa di essere un linguaggio criptico, decifrabile solo da "specialisti". Il fenomeno deriva proprio dal carattere "economico" della matematica, che si manifesta anche nel linguaggio usato. Una dimostrazione risulta preferibile ad un'altra proprio per la "rapida essenzialità" con cui giunge allo scopo. L'evitamento del superfluo diventa quindi un carattere estetico (l'eleganza) e come tale ricercato. Così accade che le parole usate negli enunciati, oltre che essenziali, nel senso di essere pregne di significato specifico, sono anche le minime indispensabili. La semplicità finale degli enunciati dei teoremi, così rigorosa e "spartana", ne rende del tutto indecifrabile il significato per la media degli studenti. Un'esperienza interessante, a questo proposito, consiste nel proporre ad un gruppo di studenti l'enunciato di un qualunque teorema geometrico o algebrico chiedendo di scrivere solamente l'ipotesi e la tesi, prescindendo del tutto dalla dimostrazione. Questo esercizio, che consiste nella semplice comprensione del significato della frase, può risultare difficilissimo e necessitare di un "allenamento" insospettabilmente lungo. Un altro interessante esempio di ciò che vogliamo dire si ha nel proporre l'enunciato del seguente teorema inserito negli ordinari programmi del I° o 2° anno di scuola superiore. 1) In un triangolo qualunque, ciascun angolo esterno è maggiore degli angoli interni non adiacenti. In modo del tutto indipendente dalla conoscenza della dimostrazione del teorema, si può accostare il primo enunciato al secondo: 2) In un triangolo qualunque ciascun angolo esterno è maggiore degli angoli interni; e chiedere in cosa consista la differenza tra i due enunciati. Si propone poi di decidere se entrambi o solo uno siano veri. Anche dopo aver appreso la dimostrazione del primo enunciato, l'unico corretto, molti studenti non trovano differenze sostanziali tra le due frasi o, quando le trovano, non riescono a pensare a una qualunque ragione che giustifichi l'inserimento della locuzione "non adiacenti" nel primo enunciato e non nel secondo o, tanto meno, esempi semplicissimi che permettano di decidere quale dei due sia "vero".
Le figure b) e c) permettono di visualizzare immediatamente che nel triangolo rettangolo e nel triangolo ottusangolo l'angolo esterno è, rispettivamente, uguale o minore del suo adiacente angolo c. Rimane in ogni caso il sospetto che tanta precisione non sia altro che una inutile e pedante pignoleria. In sostanza il linguaggio matematico risulta alquanto persecutorio. Esaminiamo più in dettaglio la caratteristica più appariscente della matematica: l'astrazione. Prendiamo in esame proprio le prime nozioni che aprono lo studio della geometria euclidea: il punto, la linea e la superficie. Si tratta dei cosiddetti "enti geometrici fondamentali", le basi su cui costruire tutto l'edificio geometrico. In genere viene disegnato con il gesso un punto sulla lavagna e viene detto che il punto materiale che tutti possono vedere non è il punto geometrico; quest'ultimo oltre ad essere completamente immateriale, invisibile, deve essere concepito come "privo di dimensioni". Il punto geometrico quindi non può mai essere "sperimentato", ma solo pensato, spogliando il punto materiale di tutti quegli elementi che costituiscono la sua realtà sensoriale. Un discorso analogo viene fatto quando si passa al concetto di linea o superficie di cui si tracciano sulla lavagna i modelli concreti:
Come nel quadro di Magritte La trahison des images, 1929, non sono la "linea" e la "superficie" geometriche. Quest'ultime sono pure concettualizzazioni, ottenute privando le forme concrete a cui si fa riferimento di tutti gli elementi concreti che possiamo constatare con i nostri occhi, e che proprio per questo dobbiamo ignorare.

Un'ulteriore difficoltà riguarda le dimensioni di questi enti, una e due rispettivamente, lunghezza e larghezza. Esse devono essere pensate come infinite, concetto che è semplicemente inconcepibile alla mente umana. La geometria inoltre, per sua natura, dispiega la sua potenza allorché le conclusioni che trae sono valide per qualunque figura pensabile diversa proprio da quella di cui ci serviamo per portare avanti la dimostrazione che, essendo concreta ed individualizzata, non è probante e non ci interessa. Siamo però costretti, per così dire, a disegnare una figura concreta, ad esempio un triangolo ottusangolo che, proprio perché tale, non può essere acutangolo o rettangolo, e a portare avanti una dimostrazione che ignori deliberatamente il fatto che si tratta di un triangolo con caratteristiche fisiche ben precise. E' necessaria quindi una deliberata astrazione dall'oggetto concreto a disposizione, cui va negata l'esistenza corporea. Desideriamo fare un passo ulteriore e puntualizzare come nell'apprendimento della matematica non sia necessaria solo una capacità di astrazione o di concettualizzazione quanto piuttosto una più sofisticata capacità di formalizzazione. Capacità quest'ultima che non si ravvisa nello stesso modo nelle ordinarie capacità di pensiero della vita quotidiana né nelle altre scienze. Definiamo capacità di astrazione la capacità di riunire in una stessa categoria concettuale enti diversi aventi gli stessi attributi comuni, fondando in questo la possibilità di conferir loro lo stesso nome, mentre riteniamo che la capacità di formalizzazione consista nella capacità di poter pensare strutture o enti astratti, i cui attributi sono ignoti e comunque ininfluenti, che vengono identificati unicamente in base al loro "comportamento" , cioè la "forma": insiemi di nessi, legami, nei confronti di altri enti o strutture nelle stesse condizioni. I "comportamenti", o le "forme" in questione, vengono descritti dal linguaggio matematico che presenta alcune caratteristiche che sembrano contrastare con il senso comune, come abbiamo cercato di evidenziare poc'anzi, che va comunque imparato. Così dopo aver appreso che : 23 = 2 . 2 . 2 deve essere possibile, ma è tutt'altro che ovvio, operare agevolmente, nello stesso modo, su: x3 = x . x . x su: (a+b)3 = (a+b) . (a + b) . (a + b) ed infine su: f3 (x) = f (x) . f (x) . f (x) che ha tutt'altro significato da f (x3). Ci sembra perciò che le specificità delle operazioni di pensiero descritte siano in parte del tutto peculiari della disciplina in questione e, a volte, decisamente contrastanti con la necessità usualmente accettata di un comune modo di pensare empirico. Vogliamo sottolineare il carattere assoluto di questa "antiesperienzialità" della matematica facendo un paragone con un esempio tratto dalla fisica. Sappiamo che, a causa della resistenza dell'aria, non è possibile constatare empiricamente la legge secondo la quale: "In un medesimo punto della Terra, l'accelerazione di caduta è costante per tutti i corpi ed è indipendente dalla loro massa". Nondimeno esiste un congegno (tubo di Newton) che permette di sperimentare anche emozionalmente l'evidenza della legge, in determinate condizioni. Nulla del genere è concepibile nella matematica, i cui enunciati sono giudizi di verità basati su inferenze logiche completamente avulse dal mondo degli oggetti. In sostanza lo scopo e la sfida matematica consistono proprio nell'escogitare e sviluppare sofisticati linguaggi formali per descrivere eventi sensorialmente percepibili al fine di eliminare, nella comunicazione dei medesimi, la limitante dipendenza dal linguaggio corrente e dagli altri ordinari metodi di trasmissione di esperienze: immagini, grafici, ecc. Ricordiamo la rivoluzione conseguente all'invenzione del metodo delle coordinate cartesiane che ha permesso lo straordinario progresso della geometria algebrica. Per citare un esempio dei più semplici: diventò possibile conoscere le mutue posizioni di due rette complanari unicamente tramite calcoli senza l'ausilio di alcun grafico. La matematica quindi non può entrare a far parte delle scienze della natura né sembra possibile inserirla tra le discipline umanistiche che l'uomo ha inventato per poter descrivere le sue emozioni ed il suo pensiero. Essa, in quanto linguaggio pur se estremamente sofisticato e formale, è una invenzione e partecipa di alcune caratteristiche del secondo tipo di discipline, ma in quanto non veicola in nessun modo i contenuti del soggetto e in quanto sottoposta a leggi rigide che la rendono adatta a descrivere i contenuti delle discipline scientifiche, partecipa della definizione dei quest� ultime. Essa si situa perciò in un'area intermedia, tra l'invenzione e la scoperta di questa invenzione medesima. L'unico oggetto che la matematica indaga è la matematica stessa, cercando di costruire un apparato per trattare le conseguenze dell'invenzione primitiva: gli enti matematici. E' in sostanza una sorta di disciplina "autoriflessiva". A questa sua natura "ambigua " facciamo risalire alcune difficoltà che si incontrano nel comprendere, ad esempio, il senso delle cosiddette "dimostrazioni per assurdo" (reductio ad absurdum ). Tali dimostrazioni consistono nel ritenere "vera" e quindi dimostrata una affermazione, A, espressa nella tesi, perché la sua opposta, non A, contraddice una qualche affermazione contenuta nell'ipotesi. L'ipotesi però non ha alcuna pretesa di veridicità oggettiva, sperimentabile come esterna al soggetto; essa è un puro convenzionalismo che diventa "vero" perché siamo tutti d'accordo nel ritenerlo "vero". L'insieme di tutte le ipotesi, di tutte le cose vere, costituisce la "realtà" esterna al soggetto, realtà con la quale il soggetto è costretto a misurarsi e in base alla quale emette giudizi di "vero" o " falso". Secondo Freud (1925 a): " La funzione del giudizio ha in sostanza due decisioni da prendere. Deve concedere o rifiutare una qualità ad una cosa e deve accordare o contestare l'esistenza nella realtà ad una rappresentazione , la qualità sulla quale si deve pronunciare potrebbe essere stata in origine buona o cattiva, utile o dannosa. Espresso nel linguaggio dei più antichi moti pulsionali orali: questo lo voglio mangiare o lo voglio sputare e, in una versione successiva: questo lo voglio introdurre in me o fuori di me...Per l'Io ciò che è reale, ciò che è estraneo all'Io, ciò che si trova al di fuori, sono in un primo tempo identici. La seconda decisione della funzione del giudizio, quella che concerne l'esistenza reale di una cosa rappresentata, interessa l'Io-reale definitivo, sviluppatosi dall'iniziale Io-piacere (Esame di realtà)... (Si tratta di stabilire) se una certa cosa, presente nell'Io come rappresentazione, possa essere ritrovata anche nella percezione (realtà). E' di nuovo, come si vede, una questione attinente al fuori e al dentro". Queste parole di Freud possono essere applicate anche quando la realtà (insieme delle ipotesi matematiche) non è la realtà concreta quotidiana, ma una realtà astratta, formale, ma pur sempre funzionante con le regole del processo secondario, cioè della logica e "percepibile" solo tramite quelle. Dobbiamo però pensare che questa realtà fittizia così congegnata risulti più "esterna" di quella naturale. Nello studio della matematica gli studenti sono continuamente sottoposti alla necessità di formulare giudizi del tipo vero-falso. Quello che appare è che la gran parte di questi studenti non arriva a porsi questo problema: essi non adottano spontaneamente alcuna procedura di controllo. Marialidia (vedi oltre) svolgeva comunemente nel modo descritto le innumerevoli espressioni aritmetiche che aveva sicuramente incontrato nel corso degli studi medi inferiori e non aveva mai notato coscientemente che quello che lei faceva era radicalmente diverso dagli altri compagni. Se si chiede agli studenti che svolgono nel modo più oltre descritto gli esercizi assegnati di escogitare qualche prova per decidere se il metodo da loro seguito può essere ritenuto "vero" o "falso", ci si può sorprendere nel notare come si manifesti una grossa confusione mentale di fronte a questa banale domanda e come risulti loro impossibile pensare a qualche semplice prova che li metterebbe in grado di decidere ed evitare alcuni grossolani errori. Ad esempio sarebbe semplice constatare che la eguaglianza (a + b)3= a3+ 3ab + b3 è errata, sostituendo sia ad "a" che a "b" il valore 1. Lo stato confusionale attraversato dallo studente, e per altro espresso anche da molti adulti ormai lontani dai banchi di scuola: "Per carità, al solo parlare di matematica mi si chiude la testa! ", fa pensare ad una sorta di trauma dovuto all'impatto emotivo con qualcosa di cui si misconosce l'esistenza cioè il "significato" della formula. Lo studente si sente costretto a confrontarsi con un "esterno", la realtà matematica, che ha delle sue specifiche organizzazioni significative, ma il "significato" per lui non è stato racchiuso simbolicamente o formalmente nelle formule, bensì è stato completamente (e difensivamente) rimpiazzato dalla formula stessa.
C) ERRORI NELLO SVOLGIMENTO DI COMPITI MATEMATICI I diversi rami dell'aritmetica: Ambizione, Distrazione, (Lewis Carroll "The Mock Turtle", in Alice in Wonderland ). Abbiamo sovente constatato che taluni studenti non riescono ad imparare la matematica pur mostrandone apparentemente il desiderio. Spesso gli insegnanti usano per questi ragazzi frasi del tipo: "Questo ragazzo non sa o non vuole ragionare! "oppure più chiaramente: "Non è intelligente!" e diagnosticano, come causa del mancato apprendimento, la mancanza o la superficialità dello studio o dell'esercizio o, talvolta, le limitate capacità intellettuali. Gli errori che questi studenti commettono in occasione di interrogazioni, compiti in classe o altre prove individuali, suggeriscono alcune ipotesi su modalità errate di ragionamento piuttosto peculiari, ma molto diffuse, che la specifica struttura della materia in questione evidenzia in modo particolare. Il primo esempio che esporremo si differenzia dagli altri perché lo studente in questione è affetto da un grave disturbo mentale. CARLO Esponiamo alcune osservazioni tratte dall'insegnamento della matematica ad un giovane di 23 anni, Carlo, studente di una facoltà universitaria. Il ragazzo, già brillante alunno di liceo scientifico, capace e interessato allo studio, è schizofrenico e viene seguito, da circa quattro anni, in terapia psicoanalitica. La malattia è insorta dopo il conseguimento del diploma di maturità. Per iniziativa del terapeuta si attua un tentativo di riprendere gli studi universitari, di fatto mai iniziati, con lo scopo di affrontare l'esame di matematica. Nel corso di queste lezioni sono state fatte alcune osservazioni che passiamo a descrivere. Spesso Carlo dovendo svolgere l'espressione: (a+b) (a-b), risponde che il risultato è 0 come se si trovasse di fronte alla somma di due termini opposti: -b +b = 0. Si può fare un'ipotesi: lo studente è rimasto più colpito dal fatto che ci siano +b e -b piuttosto che dalla struttura della operazione, che in effetti è una moltiplicazione. E' possibile che la sua attenzione sia stata catturata da quell'unico particolare, la presenza di +b e -b, a scapito di tutto il resto. Questa situazione presenta delle analogie con quella di un bambino piccolo che, osservando la buccia arancione dell'arancia dica che è il sole, ritenendo che l'uguaglianza tra il sole al tramonto e il frutto si attui sulla sola specificazione del colore (vedi il caso di Anna). Carlo riesce però a correggersi se gli si fa notare che si tratta di una moltiplicazione tra polinomi, occorre pronunciare la parola perché la sola vista dell'operazione non basta al riconoscimento. A volte occorre fare qualche segno speciale, ad esempio indicare graficamente con delle freccette la sequenza delle operazioni:
(a + b) . (a - b) = aa - ab + ab - bb occasionalmente è sufficiente accennare soltanto alle freccette con il movimento della penna perché il ragazzo riesca a risolvere l'esercizio. Carlo può non risolvere nello stesso modo due espressioni uguali presentate successivamente come se, essendo trascorsi alcuni secondi di tempo e avendo messo da parte il precedente foglietto, avesse completamente dimenticato lo svolgimento precedente e bisognasse quindi ricominciare da capo. Spesso dice: "Che fatica!", quasi fosse estenuato, oppure afferma di aver capito, mentre invece ha solo letto, come se confondesse una operazione uditivo-percettiva, come la lettura a voce alta, con la comprensione e la capacità di risoluzione. Nella lettura o nell'ascolto di espressioni algebriche vengono attuati alcuni tentativi di smontaggio delle parole che ne distruggono il senso. Se gli viene detto: "Scrivi 53" (pronuncia: cinque alla terza) scrive 5a3 (pronuncia: cinque "a" alla terza). Allora gli si ripete, scandendo bene la differenza tra le lettere e le sillabe, e gli si fa notare la differenza tra i diversi suoni. Ma sembra che quest'ultima non venga percepita. A questo punto le due espressioni vengono scritte e si chiede al ragazzo di leggerle a voce alta. Questa esperienza può non essere significativa per Carlo, allora viene richiamata l'attenzione sul fatto che ín una delle espressioni c'è una "a" in più mentre nell'altra manca e viene invitato a rileggere forte e alcune volte riesce a capire la differenza. Capita spesso che lo studente legga le precedenti espressioni nello stesso modo, per cui, ascoltando, non viene percepita alcuna differenza. La parola "alla" in questo caso viene scissa in "a" - "alla" e ciò crea confusione nel significato. Un'unica esperienza sensoriale, la vista sola o il solo ascolto della formula, non risulta sufficiente a ripristinare il significato, ma occorre ricorrere anche ad altri "segni" poiché l'integrazione dei cinque sensi è stata smontata. Trattandosi di un giovane schizofrenico, questo disturbo dell'apprendimento viene inserito nel ben più grave disturbo mentale presente. Però taluni meccanismi osservati in questo caso, che potremo chiamare "autistici" secondo il concetto meltzeriano di "smontaggio dei sensi", descritto in Esplorazione sull'autismo, sono presenti in adolescenti per altri aspetti normali. Nell'esempio che segue, tratto da un elaborato svolto in classe da uno studente di quindici anni, ci sembra arduo diagnosticare la causa dell'errore attribuendola a mancanza di studio o di esercizio. Testo: esercizio sullo svolgimento dei prodotti notevoli: (x2 - 2x + 1)2 - (x + 1) . (x - l)3 + 2 . (x - l)3 = Risoluzione dello studente: x4 - 4x2 + 1 - (x + 1) (x3 - 3x2 + 3x) + 2 (x3 - 1) = ... Come si può notare, il ragazzo risolve la stessa espressione ( x - 1 )3 una prima volta in un modo: (x - 1)3 = x3 - 3x2 + 3x, si è cioè accorto che si tratta di un prodotto notevole (anche se la formula trascritta è errata) e una seconda volta in un altro modo: (x - 1)3 = x3 - 1. Nulla in questo caso fa supporre che il ragazzo sia consapevole di avere a che fare con un prodotto notevole. Sorge un dubbio: lo studente ha riconosciuto i prodotti notevoli? Ha forse dimenticato le regole di svolgimento? Ci sembra difficile fornire una risposta a queste domande. Sembra addirittura che lo studente abbia attraversato "un momento di cecità" nel senso che non ha riconosciuto come uguali le parti sottolineate. Durante lo svolgimento dell'esercizio le sue "facoltà mentali" sembrano peggiorate e alla fine non riconosce neppure il prodotto notevole che poco prima sembrava aver consapevolmente individuato. Gli studenti che fanno spesso errori del genere descritto fanno spontaneamente sorgere dubbi sulle loro capacità di usare in modo integrato la vista o l'udito, o anche la memoria a breve o a lungo termine. Quindi l'osservazione che ha dato origine a queste riflessioni: "Questi studenti non riescono a ragionare", può essere riformulata in questi termini: questi studenti non fanno collegamenti, smontano o usano in modo estremamente ridotto e non integrato i sensi.
MARIALIDIA Osserviamo lo svolgimento di un'espressione aritmetica ad opera di una studentessa quattordicenne di primo anno di scuola media superiore, Marialidia. Testo: riepilogo sulle espressioni aritmetiche (- 10 + 1/20) : [ [ -0.6 - (25/2 + 9/4)] - [ -6 - (4/5 - 7/5)] ] = Svolgimento corretto: -199/20 : [[ - -199/20 : [(-12 - 295) /20 + 27/5]= -199/20 : [(-307/20 + 27/5] = -199/20 : [(-307 + 108)/20]= - (-1) .(-1) = 1 Svolgimento di Marialidia : (- -6/5 : [[- -6/5 : [[-1 / 63 1 / 1 : 1 = 1 (N.B. Per esigenze tipografiche, nella semplificazione dei fattori, siamo stati costretti a sostituire il trattino orizzontale (-) alla lineetta obliqua (/) usata normalmente.) Questa modalità di risoluzione visivamente simile a quello di uno svolgimento corretto, non segue alcuna regola del calcolo matematico. Se l'esercizio fosse un lavoro artistico potrebbe essere accostato all'opera Poesia di Man Ray. Richiama alla mente, per associazione, la "ricostruzione delirante" di avvenimenti incomprensibili, perché troppo dolorosi, attuata da pazienti psicotici. Gli esercizi svolti, con calligrafia nitida ed ordinata, tutti in questo modo senza avvertire alcuna differenza con i lavori dei compagni e dell'insegnante, erano del tutto errati, ma gli errori non erano quelli tipici degli studenti in questi casi, bensì totalmente peculiari.
Sembrava che Marialidia ignorasse totalmente il significato dei simboli e dei segni matematici. Le domande volte a stabilire i criteri da lei seguiti nello svolgimento risultavano incomprensibili alla studentessa che sembrava ignorare l'esistenza di regole e operazioni e sosteneva di ottenere molto spesso il risultato del libro. La ragazza aveva frequentato le scuole elementari e medie considerando l'aritmetica prima e l'algebra poi un cumulo di regole inutili e incomprensibili. L'unica caratteristica che aveva recepito era l'aspetto percettivo della semplificazione delle espressioni aritmetiche che riusciva a riprodurre come un disegno.
D) ERRORI NELLE STRATEGIE PER AFFRONTARE UN PROBLEMA NUOVO Vediamo ora un altro esempio: vengono spiegati i prodotti notevoli: quadrato e cubo di binomio, quadrato di un trinomio e vengono svolte abbondanti esercitazioni. Il giorno della prova in classe viene proposto, oltre ad esercizi che riguardano l'applicazione di prodotti notevoli già conosciuti, il calcolo di: (a + b + c)3 cubo di un trinomio Subito gli studenti dicono che quel prodotto notevole non è stato spiegato e l'insegnante ribatte che con le conoscenze già acquisite, ragionando un pochino, possono risolvere il quesito. Gli studenti che pensano di intravedere una possibile soluzione e tentano di trovarla, seguono tre strade: 1) (a + b + c)3 = (a + b + c)2 . (a + b + c) = .... svolgimento dei calcoli. 2) (a + b + c)3 = (a + b + c) (a + b + c) (a + b + c) = ... svolgimento dei calcoli. 3) (a + b + c)3 = a3 + b3 + c3 + 3ab + 3ac + 3bc Le prime due strade possiamo definirle corrette, la prima addirittura elegante in quanto consente un minor numero di calcoli. In entrambi i casi lo studente si rende conto che le formule già conosciute non servono in quanto inadatte a risolvere il problema, ma si può arrivare alla soluzione nello stesso modo ricorrente che è stato usato, ad esempio, per conoscere: (a + b)3 = (a + b)2 (a + b) o per conoscere (a + b + c)2 = (a + b + c) (a + b + c). Ritengono insomma che (a + b + c)3 si comporti come una qualunque altra potenza di binomio già nota, per la quale, svolgendo determinati calcoli, sarà possibile ricavare una formula. Gli studenti che hanno scelto la terza via invece non hanno potuto riconoscere che le formule già note erano inservibili perché nella loro mente una formula non rappresenta l'abbreviazione di un procedimento lungo, ripetitivo e faticoso, del quale costituisce il risultato finale, utile in quanto "economico", ma la formula e il prodotto notevole sono la stessa cosa. Quindi hanno ritenuto che nella espressione (a + b + c)3 si potesse prendere la formula da loro conosciuta per il quadrato di un trinomio: (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc e sostituire semplicemente il valore 2 con il valore 3. Richiesti di una spiegazione sul perché del loro operare non sono in grado di fornire alcuna spiegazione se non la frase: "Ho creduto che si potesse fare così... mettere al posto del 2 il 3". Oppure più semplicemente: "Ho pensato che si dovesse fare così!". I procedimenti matematici, nella loro fantasia, non hanno un significato intrinseco ma seguono leggi di "sequenzialità" e "continuità", cioè regole percettive. Se si domanda loro come si può fare per decidere se l'espressione da loro scritta sia vera o falsa, sembrano non avere alcuna idea di procedimenti semplicissimi che permetterebbero di appurare rapidamente quanto richiesto. Questa incapacità a fornire "procedimenti" che permettano di decidere se un'uguaglianza algebrica sia vera o falsa dipende dal fatto che lo studente considera la formula matematica come un oggetto concreto indivisibile, concezione questa che fa pensare al lavoro di H. Segal sull'equazione simbolica del pensiero psicotico. A volte gli studenti, dopo la spiegazione, dichiarano di aver capito; ben presto ci si rende conto che questa frase significa soltanto: "Per motivi del tutto misteriosi ho capito che non dovevo fare così", ma non corrisponde a una reale comprensione. Possiamo dire che lo studente recepisce la spiegazione ottenuta sotto l'aspetto "morale" piuttosto che "conoscitivo", in quanto sembra considerare la disciplina matematica come un elaborato sistema di regole, staccate le une dalle altre (come un decalogo comportamentale), e non come una metodologia di indagine o una coerente ed utile invenzione, ad esempio come un linguaggio avente significato. I giudizi di "vero" o "falso" basati sul contesto vengono sostituiti da giudizi moralistici o da spiacevoli sensazioni di colpa e di inadeguatezza. Questo comportamento emotivo che impedisce di usufruire delle spiegazioni e delle correzioni richiama alla mente alcune formulazioni della concezione di W. Bion. Gli studenti che fanno gli errori descritti considerano le formule come "cose in sé", separate dal significato da cui provengono. Esse permangono nella mente come "elementi ß" a guisa cioè di corpuscoli indigeriti, se vogliamo seguire la metafora alimentare usata spesso dagli insegnanti nei confronti di alcuni studenti che si lamentano di aver molto studiato senza apprezzabili risultati: "Hai studiato tanto ma devi ancora digerire quello che hai studiato! ". Durante le correzioni degli errori da parte degli insegnanti, queste formule = elementi ß, sembrano arricchirsi di un'ulteriore qualità persecutoria, per cui diventano per lo studente un "oggetto bizzarro": ciò che era difficilmente comprensibile e oscuro nelle sue motivazioni profonde e perciò preoccupante di per sé, si colora inoltre di spiacevoli sensazioni di colpa o vergogna. Spesso questi studenti, infatti, cercano di evitare le spiegazioni e le delucidazioni sugli errori fatti che, dal loro punto di vista, non hanno altro scopo se non quello di accrescere le sofferenze.
E) MODI DI ORGANIZZARE NELLA MENTE LE NOZIONI APPRESE Facciamo ora alcuni esempi nei quali, da parte di alcuni studenti, viene organizzata la conoscenza già acquisita.
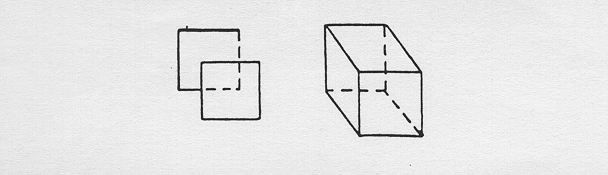
ANNA Il seguente episodio è tratto dal materiale emerso nel corso della terapia di Anna, una bambina di poco più di undici anni, venuta in terapia per gravissimi disturbi di apprendimento. Anna, pur scrivendo e leggendo abbastanza correttamente, non è in grado di comprendere il significato delle frasi più semplici e quindi non impara nulla in nessuna disciplina e specialmente in matematica. L'episodio descritto avviene in seduta, circa un mese dopo l'inizio della terapia. Due o tre sedute prima di quella descritta, la ragazzina aveva deciso di fare un disegno di "forme geometriche" tra cui il cubo, senza alcun modello. Si è potuto notare che conosceva il modo classico di disegnare il cubo, anche se non rispettava la lunghezza degli spigoli.
Nella seduta odierna, Anna scopre nella sua scatola personale di materiale da gioco, quattro cubi di legno colorato di tre cm. di lato. Due cubi sono blu, uno è rosso e l'ultimo è giallo. Decide di disegnarli, per cui prende un foglio dall'album e pone davanti a sé il cubo blu per ricocopiarlo. Di fronte al cubo concreto esegue un disegno del genere.
Lei stessa rimane perplessa di fronte al risultato che cerca di correggere con varie cancellature e rifacimenti senza esito. Dopo un momento di silenzio chiede al terapeuta: "Sono cubi o dadi?"... "Qual è la differenza?" le si domanda. Anna risponde che i dadi hanno i puntini con i numeri. Le viene detto allora che tutti i dadi sono cubi. A questo punto Anna afferma decisa: "Sono cubi!". Pronunciata la "parola magica" può disegnare il cubo nel modo già illustrato ed appreso a scuola, usando il righello apparentemente per prendere le misure ma in realtà senza tenerne conto, per cui nessuna faccia del cubo è un quadrato. Mette da parte il cubo blu, si pone davanti quello rosso e, guardandolo attentamente, ripete lo stesso procedimento. Così fa pure con quello giallo e con il secondo cubo blu, nonostante siano tutti identici per forma e dimensione. Mette poi i cubi già disegnati uno sopra all'altro, formando come una torre. Colora le quattro figure seguendo l'ordine dei colori dei cubi della torre e ne ripassa i contorni con la penna, senza tener conto degli spigoli visibili e di quelli nascosti. Questi meccanismi così evidenti in Anna sono pur tuttavia presenti in moltissimi studenti più grandi, "normali" e con rendimenti accettabili nelle altre discipline scolastiche. Qualche esempio: vengono spiegate le equazioni e numerosi studenti sembrano essere in grado di averne appreso il significato concettuale e il procedimento pratico di risoluzione. Si presenta ora un quesito riguardante un argomento di fisica o chimica risolvibile con un'equazione. La maggior parte degli studenti non è in grado di riconoscere nelle espressioni scritte alla lavagna un'equazione; se però si cambiano i simboli sostituendo ad esempio alle grandezze fisiche incognite, t = tempo o s = spazio, la x, oppure si pronuncia la parola equazione, tutti come magicamente si mettono in moto e riescono a risolvere correttamente il quesito. Diciamo che la nozione "equazione e sua risoluzione" è depositata in forma meccanica in qualche "luogo" della mente ed è richiamabile solo con certi "bottoni-stimolo". Il concetto perciò non è mobile e usabile in modo elastico quando serve, ma è fisso come un blocco compatto. Il suo riconoscimento è legato a certi parametri percettivi: denominazione, forma dell'incognita, posizione nello spazio ecc. Un altro esempio significativo di questo fenomeno è il caso di studenti che riescono a risolvere un'equazione di I grado solo se l'incognita si trova a destra e non a sinistra o viceversa. Per alcuni alunni l'espressione 2x = 10 è risolvibile immediatamente, in quanto viene riconosciuta come equazione, mentre l'espressione 10 = 2x non lo è. Essi trasportano l'incognita da destra a sinistra, operando naturalmente vari cambiamenti di segno, aumentando quindi le possibilità di errore e infine riconoscono qualcosa di noto, nel senso che possono risolverlo tranquillamente in modo automatico. Questi comportamenti cognitivi e molti altri che possono essere osservati, ci mostrano un modo di apprendere parcellizzato, meccanizzato e non integrato assolutamente, dove ogni pezzetto di conoscenza è separato dagli altri; le nozioni si ammassano alla rinfusa in zone della mente come oggetti nei cassetti senza alcuna comunicazione tra loro. Questo stadio può essere considerato normale per l'apprendimento di un concetto se ne costituisce una breve tappa evolutiva. Per passare alla tappa successiva bisogna affrontare un procedimento mentale simile a quello che Bion descrive nella "opacità della memoria e del desiderio", che in questo caso consiste nell'abbandonare tutto ciò che è sensoriale: cioè ad esempio la scrittura dell'incognita usata (a, b, t, x o y) la sua posizione sul foglio ecc. per cogliere invece le congiunzioni costanti e le strutture delle relazioni. Nell'apprendimento della matematica è necessario riuscire ad "astenersi" dalla gratificazione sensuale data dalla percezione sensoriale. Le operazioni mentali di astrazione e ancor più di formalizzazione, imponendo di abbandonare il noto ed il concreto per l'ignoto e l'astratto, implicano per questo la tolleranza della mancanza dell'oggetto e di per sé causano dolore mentale. Si ha l'impressione che molti studenti, non sopportando questa deprivazione sensoriale, cerchino di ricostruire l'oggetto concreto che hanno perduto in quanto se ne sono dovuti astenere. Il risultato è un'aderenza assoluta ad un procedimento ossificato. Moltissimi studenti sembrano in generale preferire procedimenti lunghi, monotoni, ripetitivi anche percettivamente che, diventando automatici, richiedono poca "attenzione" e poco "ragionamento", a procedimenti brevi, sintetici, con pochi calcoli che richiedono però capacità attiva di recepire somiglianze, differenze, comprensione di regole e capacità di sintesi. Ad esempio, dovendo eseguire il calcolo di questa espressione (x + 1)3 (x - 1)3 procedono così: (x3 + 3x2 + 3x + 1) (x3 - 3x2 + 3x - 1) = x6+... disponendosi ad una moltiplicazione di ben 16 termini, lunga e faticosa, e per questo soggetta ad errori ma eseguibile passivamente, mentre non colgono o non vedono il vantaggio di poter fare (x + 1)3 (x - 1)3 = [(x + 1) (x - 1)]3 = (x2 - 1)3 = ..... trasformazione che permetterebbe di risolvere molto rapidamente il quesito. L'attenzione e la concentrazione risparmiate con la prima modalità risolutiva devono evidentemente rimanere disponibili per altri scopi. Ci sembra quindi che la funzione dell'attenzione acquisti una grandissima importanza proprio nel suo costituirsi come una "facoltà attiva" verso l'esterno. Secondo Freud (1911) infatti: "Viene istituita una funzione particolare per esplorare periodicamente la realtà esterna, così che i dati di questa siano già noti quando si produce un incontenibile bisogno interiore e cioè la funzione dell'attenzione". Meltzer dedica tutta la prima parte del suo lavoro Esplorazioni sull'autismo alla funzione dell'attenzione: "La maggior parte degli oggetti "ricevono attenzione". Noi tendiamo a sperimentare un tale "dispiegamento" dentro di noi come un processo attivo". L'esercizio di questo "processo attivo" è per taluni studenti particolarmente difficile e faticoso. Spesso si ha l'impressione che utilizzino la loro capacità mentale nella maniera più "economica" possibile in modo che i contenuti mentali, una volta che siano stati percepiti e codificati, siano in grado di "riprodursi" in un certo senso autonomamente, cioè senza necessitare di attenzione. Questo funzionamento automatico della mente presenta la caratteristica di evolvere nel verso di un sempre più grande impoverimento. L'automazione sembra cristallizzarsi e parzializzarsi occupando uno spazio mentale sempre più rigido. Le facoltà sensoriali come vista e udito o anche quelle mentali come l'attenzione per percepire o la concentrazione sembrano diminuite o, a volte, addirittura mancanti. Ad un osservatore esterno questi studenti sembrano comportarsi con la propria mente in modo da rendere il suo funzionamento il più meccanico possibile, effettuando una sorta di "istituzionalizzazione" del pensiero. Per illustrare ciò che accade alla loro mente potremmo adoperare le stesse parole che Bion (1976) utilizza per descrivere l'istituzione: " ... Un' istituzione si comporta secondo certe leggi e regole - deve stabilirle - e tutte le leggi organizzative diventano rigide e definitive come le leggi della fisica. Un' organizzazione diventa dura ed inanimata come questo tavolo. Io non conosco chi sia in grado di dire a che punto ciò che è animato diventa inanimato ... ". Possiamo dire che questi studenti hanno con parti della propria mente un rapporto contenitore-contenuto che possiamo definire "molto rigido" a causa della loro tendenza a "istituzionalizzare" in questo senso deteriore la conoscenza. Studenti di questo tipo, íl cui numero è molto più grande di quanto si creda comunemente, se richiesti esplicitamente, dicono di aver capito quanto spiegato, raramente pongono domande e sembrano paradossalmente opporsi alle spiegazioni supplementari. Hanno grandi difficoltà a collegare i concetti, a fare paragoni, a riconoscere le uguaglianze di strutture e a porsi in modo attivo e riflessivo di fronte ad un compito complesso. Le loro difficoltà aumentano quanto più la scienza si formalizza e viene richiesta una partecipazione ed un impegno autonomo. Questi studenti, molto passivi, nel senso sensoriale e mentale del termine, ma, a volte molto assidui, sembra che si aspettino di apprendere mediante procedimenti molto primitivi, come una sorta di osmosi (o di assorbimento) con la situazione scolastica nel suo complesso, una modalità di apprendere quasi "parassitaria". Questa situazione, attivata specialmente dalla condizione gruppale durante le spiegazioni dell'insegnante, può essere interpretata come una massiccia dipendenza accoppiata ad una magica onnipotenza, e trova il suo punto di rottura traumatica nelle prove individuali che lo studente affronta e che vive con grande angoscia. Spesso in queste situazioni (interrogazioni, compiti in classe, domande estemporanee) possono essere osservati quei fenomeni dei quali abbiamo già parlato come mancanza di osservazione o di ragionamento logico che danno l'impressione di avere a che fare con una persona che non riesce a usare agevolmente la sua mente e le sue funzioni. E' possibile che questi meccanismi di pensiero siano peculiari dell'ambito matematico e si evidenzino solo in quelle circostanze? Non abbiamo una risposta per questa domanda. E' certo però che la disciplina matematica nei suoi vari livelli sembra evidenziare i limiti delle possibilità di pensare in modo logico formale di ciascun individuo.
Le domande scaturite dalla discussione degli errori, ed esposte a commento dei medesimi, possono indurre ad ipotizzare un disturbo nell'area simbolica degli autori degli errori paragonabile a un disturbo psicotico: di fronte ai compiti della matematica che richiedono una prestazione altamente simbolica, il soggetto prova un dolore mentale non gestibile. Si mette in moto un meccanismo difensivo specifico che evita il dolore ma ha una conseguenza: viene costruita una "nuova realtà" che è soltanto realsimile a livello percettivo, come nel caso di Marialidia, ma che misconosce la realtà "vera", cioè l'esistenza del significato delle formule e del linguaggio matematico in genere.
Marialidia, data la particolarità del suo modo stravagante di risolvere le espressioni matematiche, sembra fornire soluzioni "psicotiche" a problemi dove gli altri studenti danno soluzioni "nevrotiche".
La vastità e generalità del fenomeno descritto porta a cercare delle spiegazioni eziologiche generali e induce a supporre che nella storia personale di questi studenti ci siano elementi tali da far pensare a dei danni nei processi di simbolizzazione e, naturalmente, i modelli teorici con i quali questi danni possono essere descritti o spiegati sono molteplici.
Andiamo a cercare in Inibizione, sintomo e angoscia .(1926) e più precisamente nell'appendice C, "Angoscia, dolore e lutto", il collegamento che Freud trova tra i concetti di dolore, dolore mentale, angoscia e lutto, che è fondamentale al nostro proposito. L'appendice C comincia con un'affermazione che può essere sottoscritta ancora oggi. Freud dichiara che è molto poco ciò che ci è noto sulla psicologia dei processi emotivi. Egli dice però di essere portato a concludere che l' angoscia sia una reazione al pericolo di perdita di un oggetto. Ma la reazione alla perdita di un oggetto è stata identificata con il lutto (1917). Nella discussione di questo processo il peculiare dolore che il soggetto prova risultava inspiegabile agli occhi dell'autore. Egli in questo frangente si domanda: "quando la separazione da un oggetto produce angoscia, quando produce un lutto e quando produce, forse, solo dolore?". L'elaborazione successiva esegue un'ipotetica ricostruzione genetica. La situazione di perdita della madre, se coincide con una sensazione di necessità, si configura nel bambino piccolissimo come una situazione traumatica. Se questo bisogno non è presente si profila una situazione di pericolo. Il primo elemento determinante dell'angoscia è quindi la perdita della percezione dell' oggetto, che diventa equivalente alla perdita dell'oggetto. A questo punto dell'ipotesi genetica, angoscia e dolore sono insieme poiché il soggetto non discrimina tra assenza temporanea e perdita definitiva. Solo dopo che un "oggetto" si instaura e caratterizza compiutamente, che acquista un senso la perdita dell'amore dell'oggetto, che con esso ci sono legami di desiderio, è possibile riferirci alla reazione di dolore come l'attuale reazione specifica alla perdita dell'oggetto. La reazione di angoscia corrisponderà allora alla reazione al pericolo che comporta la perdita dell'oggetto, o più direttamente al pericolo della perdita dell'oggetto. Non può sfuggire a Freud, tuttavia, che il dolore stesso ha ricevuto varie interpretazioni nel suo pensiero e che non è facile stabilire un collegamento tra il dolore provocato dall'irruzione di uno stimolo che deborda lo schermo protettivo contro gli stimoli, il dolore procedente da stimoli interni e il dolore causato dalla perdita di un oggetto. Egli si appella al comune uso linguistico che "ha creato la nozione di dolore interno, mentale, e ha trattato il sentimento di perdita di oggetto come equivalente al dolore fisico". La continuità e la transizione dal dolore fisico al dolore mentale verrà giustificata nella teoria facendo uso del concetto di narcisismo: questa transizione corrisponde a un cambiamento dall'investimento narcisistico all'investimento di oggetto. Rimane da legare un'altra importante reazione emotiva alla perdita di un oggetto, il lutto. Esso avverrà sotto l'influenza del test di realtà. E' il soggetto stesso che deve separarsi dall'oggetto, dice Freud, giacché esso non esiste più. E la fatica sarà dura e prolungata in quanto egli dovrà disfare, attraverso il ritiro di ingenti investimenti, tutti i legami che lo univano all'oggetto. La condizione estremamente dolorosa di questo processo trova spiegazione nelle ipotesi elaborate precedentemente.
Questa teoria complessiva sugli affetti, sul dolore, l'angoscia, il lutto, può ovviamente essere discussa e contrastata sia dall'esterno, con una critica generale a molti presupposti genetico-evolutivi freudiani (critica portata avanti da molti altri modelli psicoanalitici e no), che dall'interno, in quanto è evidente, in primo luogo allo stesso autore, che lascia molte domande senza risposta. M. Klein (1931), che studiò approfonditamente i disturbi di simbolìzzazione ("base di tutti i talenti") osservando il gioco dei bambini piccoli, attribuì le difficoltà a giocare e ad imparare alle angosce persecutorie riguardanti le fantasie sessuali relative al rapporto tra i genitori, all'oggetto combinato e alla scena primaria. Così, ad esempio, un disturbo di apprendimento come l'incapacità ad eseguire le comuni operazioni aritmetiche, veniva interpretato come una difesa relativa alle fantasie sul coito dei genitori. H. Segal (1957), fece risalire la non differenziazione tra la cosa simbolizzata e il simbolo ad un disturbo nella relazione tra l'Io e l'oggetto; in conseguenza del conflitto, il simbolo, regredito a equazione-simbolica, verrebbe usato per negare la perdita dell'oggetto piuttosto che per superarla. Tra gli psicoanalisti postkleiniani, W.R. Bion (1962a), nella sua teoria sulla nascita e lo sviluppo del pensiero, pose in connessione i disturbi dell'apprendimento, e della capacità di pensare in genere, alle difficoltà insorte nella relazione madre-bambino. Il problema che si pone Bion continuativamente, in tutti i suoi scritti è quello di "come trattare i pensieri" ovvero i protopensieri (impressioni sensoriali ed emotive), che scaturiscono nell'infante quando si confronta con le sue percezioni interne ed esterne, positive e negative. Il compito di risolvere la questione (capacità di pensare) viene attribuito ad una particolare funzione della mente la funzione <<alfa>>. Questa funzione (che dobbiamo pensare come potenzialmente innata e in azione già nella vita intrauterina), agisce sulle impressioni sensoriali ed emotive che "impattano" sull'infante nel suo contatto con il mondo esterno, trasformandole in elementi alfa suscettibili di reciproci collegamenti mentali, nessi logici, strutturazioni trasformative, così queste divengono adatte ad essere usate come "mobilia" deì sogni, dei pensieri diurni, dei ricordi ecc.
In sostanza il corretto funzionamento della funzione alfa è legato al normale, consapevole e condiviso rapporto con la realtà interna ed esterna. Se la funzione alfa fallisce, queste impressìoni rimangono, allo stato grezzo, come corpuscoli indigeribili, detti elementi B, privi della possibilità di formare legami, nessi logici o strutturazioni trasformativi tipiche dei processi secondari del pensiero. In questo caso la capacità di pensare risulta menomata e s'instaura quello che viene definito "disturbo del pensiero", dovuto all'installarsi nella mente dell'individuo di un "oggetto che fraintende". Come affronta una situazione di mancanza di oggetto un bambino che deve comunque essere nutrito al seno e che per difetti individuali e/o per carenze di réverie materna non riesce a tollerare l'assenza dell'oggetto? Secondo Bion il bambino compirebbe una particolare scissione che consiste nell'usufruire della comodità materiale rappresentata dal seno senza riconoscerne la sua provenienza animata: il seno quindi fornirebbe un servizio. Si tratta di una operazione di deanimazione che distacca il seno soprattutto dalla sua capacità di provare amore e interesse per il bambino, unica ragione per cui il bambino viene allattato, curato ecc.
I filoni di ricerca summenzionati portano a collocare gli errori nell'ambito delle difese messe in atto per fronteggiare il dolore dovuto alla perdita dell'oggetto primario che viene, per così dire, riattualizzata di fronte ad un compito nel quale la natura astratta e formale rappresenta la caratteristica essenziale.
Molti degli errori riscontrati possono essere considerati come un esito di questo particolare tipo di scissione e di un funzionamento difettoso della funzione alfa. Spesso si assiste ad un aumento di esuberanza fisica, di irrequietezza usata come una primitiva difesa muscolare nei confronti di stimoli mentali vissuti come oggetti concreti. Le correzioni, i tentativi di stabilire dei nessi, vengono associati a sensazioni spiacevoli di tipo persecutorio, vissute dallo studente che ha l'impressione di aver "fatto qualcosa di male" in senso generico, sensazioni che ostacolano il miglioramento. Potremmo dire, usando il linguaggio bioniano, che la capacità di apprendere risulta impedita poiché lo studente sembra avere a che fare non più con "oggetti matematici", cioè impressioni sensoriali ed emotive su cui esercitare i fattori della funzione alfa>>, bensì con "oggetti bizzarri" vale a dire con elementi della realtà carichi di spiacevoli connotazioni persecutorie (frammenti di Super-lo).
L'incapacità di comprendere può allora essere descritta come un "attacco al legame" che una parte della mente, quella parte che "fraintende", Sferra contro un'altra sua parte. Gli aspetti imitativi, concreti e massicciamente ripetitivi dei procedimenti errati adottati, hanno sovente la funzione "allucinatoria" di riprodurre l'oggetto perduto senza tenere conto della sua assenza. Dovremmo allora ipotizzare che lo smontaggio dei sensi non è peculiare solo dello stato autistico o puramente schizofrenico, ma è un meccanismo suscettibile di essere attivato, anche in assenza di una specifica patologia, in talune circostanze, laddove vengano richieste prestazioni di un grado elevato di astrazione. E' possibile pensare che il gran numero di regole matematiche (dei segni, delle parentesi, delle operazioni ecc ... ) necessarie per svolgere una espressione algebrica, qualora non organizzato in una "forma narrativa" tramite il significato e i reciproci legami, agisca sulla mente come una gran massa di stimoli indifferenziati, indistinguibili e insensati. Lo studente allora vaga da un'ipotesi operativa ad un'altra senza riuscire ad ancorarsi a nessuna, poiché tutte equivalenti o tutte differenti su base percettiva e non significativa, come nel caso degli studenti che risolvono le equazioni solo se l'incognita si trova nella parte sinistra della eguaglianza.
Ci sembra opportuno a questo punto specificare il significato con cui abbiamo usato le locuzionì: "equazione simbolica" di H. Segal, il termine "pensiero psicotico" o meccanismo "delìrante", ecc.
In sostanza da un'eguaglianza di "forma" sensorialmente percettibile si è passati a un'uguaglianza di significato delle due azioni. Noi definiamo psicotica una mente che ragioni in questo modo se si tratta di una mente adulta in un dato contesto culturale.
In un bambino piccolo, per un dato periodo di tempo, i "nomi" e le "cose concrete" che essi denominano coincidono. Il nome "papà", ad esempio, indica per un certo tempo il solo papà del bambino, quasi come un'attribuzione personale del bambino stesso (papà mio); solo in un secondo tempo viene concepito come la denominazione condivisa di una serie di funzioni relazionali e parentali che fanno sì che ogni bambino abbia il "suo" papà. Tutto ciò ci sembra analogo alla "impressione" di taluni studenti che (a2 + 2ab + b2 ) non sia il risultato di determinati calcoli e operazioni già presenti nella indicazione (a + b)2 ma che (a + b)2 sia uguale a (a2 + 2ab + b ) come un'identità in sé compiuta. Tutto questo a prescindere dallo svolgimento, cioè dalla struttura di risultati funzionali che permettono di trovare, usando le stesse operazioni e funzioni, il "nome matematico", cioè le formule di (a + b)3 o (a + b)4 ecc... Questi modi di ragionare, analogamente a quanto descritto in precedenza, li definiamo "psicotici", intendendo con questo termine una particolare modalità di pensiero o di meccanismo mentale, che assume talune caratteristiche non specifiche solo di pazienti con gravi patologie mentali, ma altresì presenti comunemente in bambini piccoli o in individui di altri contesti culturali. Un ulteriore esempio servirà a chiarire ciò che intendiamo dire. In alcune tribù primitive quando un individuo muore, è uso cancellare dal linguaggio tutte le parole che hanno una qualche attinenza con il nome del defunto sostituendole con nuove locuzioni. Questa specifica modalità di reagire al dolore e al lutto risulta condivisa dall'intera tribù e come tale consona al sentire individuale.
Lo stesso comportamento, in contesti completamente differenti e attuato da individui isolati, produce serie difficoltà nella vita di chi ne fa uso, viene giudicato inadeguato dai più come mezzo per fronteggiare i sentimenti di dolore e di lutto che dovrebbe affrontare, e induce a sospettare una grave patologia mentale. In ogni caso desiderando usare la parola "meccanismo di pensiero psicotico" per l'analogia che abbiamo testé descritto, intendiamo privarla di ogni connotazione indicante una qualche patologia mentale nel senso usuale del termine, in quanto fuorviante rispetto ai nostri scopi. Gli studenti di cui ci occupiamo ragionano in modo "psicotico" in un ambito culturale molto particolare, quello matematico, nel periodo di tempo nel quale sono costretti a misurarvici, cioè nelle scuole medie superiori. E' in questo ambito che subiscono tutte le conseguenze della loro "malattia mentale" che possiamo osservare nei comportamenti descritti. Gli errori che abbiamo segnalato sono frutto di modalità di pensiero che se fossero applicate alla realtà e al linguaggio naturale sarebbero giudicati indizi di una qualche patologia mentale. Nella realtà e nel linguaggio matematico conducono ad errori che non dipendono solo da scarsa conoscenza delle regole, dei teoremi o dell'argomento, insomma da scarsa applicazione allo studio, ma più precisamente da modalità errate di pensiero che, per analogia, abbiamo definito psicotiche. Vogliamo sottolineare che sono proprio tali modalità di pensiero che impediscono a questi studenti di studiare e quindi di apprendere e non viceversa.
Ciò che più conta [per il bambino] I modelli teorici sopra accennati attribuiscono il processo, per cui l'interesse dell'infante si trasferisce da un oggetto primario ad uno secondario, sia al conflitto di forze che ostacolano o vietano l'interesse per l'oggetto originale sia alla perdita reale dell'oggetto. Viene così valorizzato il significato della disillusione come spinta, di tipo paranoico o riparativo, verso lo sviluppo e l'attività mentale. Una psicoanalista inglese, Marion Milner (1955), pur condividendo la stessa linea di pensiero, sostiene la fondamentale importanza della motivazione positiva connessa con la creazione del simbolo stesso: occorre dare maggior spazio alle modalità con cui il bambino cerca di stabilire un rapporto con l'oggetto e con la realtà, oltre a quelle con cui cerca di ricostruire l'oggetto danneggiato una volta che con esso sia stato stabilito un rapporto. La Milner esamina i processi simbolici partendo dal primo pensiero prelogico e dalle condizioni con cui l'oggetto primario e quello secondario sono fusi ed avvertiti come una cosa sola, vale a dire "i momenti in cui l'originale poeta nascosto in ciascuno di noi creò il nostro mondo esterno". Concetti chiave sono: fantasia, giacché questo fenomeno può accadere solo nella fantasia, illusione, dal momento che la persona che produce la fusione crede che l'aspetto secondario sia quello primario, ansia, è l'ansia per l'oggetto originario (della rappresaglia o della perdita) che porta alla ricerca del sostituto, estasi, che rappresenta l'esperienza emotiva (l'eureka!) del trovare il sostituto.
Queste condizioni si realizzano nel gioco infantile usato come mezzo di scoperta della realtà e del limite e nelle "esperienze estatiche" che il bambino prova nel gioco medesimo.
Questo punto di vista riguardo allo sviluppo dei processi di simbolizzazione potrebbe far ipotizzare che le difficoltà a pensare degli studenti in questione siano attribuibili alla mancanza di facilitazione (intesa come opportunità fornita dall'oggetto) nel passaggio graduale da uno stato mentale in cui l'oggetto è sentito parzialmente esterno ad uno in cui è concepito stabilmente come esterno. Ci possiamo allora domandare se il fatto che un linguaggio altamente astratto, quale quello matematico, appaia intollerabile ed autoritario come una prigione e completamente estraneo agli interessi del soggetto, non sia dovuto alla circostanza che non venga sentito come malleabile e tale da consentire emozioni estatiche: un linguaggio destinato a suscitare ammirazione per la sua potenza comunicativa non comunica nulla a chi non riesce a sostenere la fatica di apprenderlo sentendola come una privazione piuttosto che come una possibilità di sviluppo. Nell'apprendimento della lingua madre ad esempio, la comprensione da parte della madre dei balbettamenti del figlio, ed il suo "dar loro un senso", s'inseriscono in una unità fusionale dove il linguaggio inizia come comunicazione per lo più privata, quasi esclusiva della coppia madre-bambino, all'insegna del gioco e delle fantasie primitive onnipotenti e fusionali. Sul versante patologico, il mutismo elettivo delle coppie gemellari o dei bambini che subiscono un trauma narcisistico evidenze le drammatiche esigenze della coppia simbiotica e getta luce su uno stadio di sviluppo nel quale soggetto ed oggetto sono parzialmente distinti e la "cosa" ed il simbolo (codice) coincidono.
L'apprendimento delle lingue morte, non destinate allo scambio verbale, o di una qualunque lingua straniera, procede naturalmente in modo diverso, con la presentazione di regole grammaticali e sintattiche già codificate. Inoltre la matematica, affine in questo alle discipline scientifiche, viene proposta, e non può essere altrimenti, in una forma che non è mai quella con la quale la disciplina stessa si è sviluppata nel corso dei secoli. La risoluzione di un problema, noto nella sua formulazione fin dall'antichità, o la sistemazione organica di una teoria la cui elaborazione completa ha richiesto centinaia di anni, viene presentata agli studenti nella sua forma finale, raffinata dai tentativi errati e dalle ridondanze che hanno contribuito comunque al raggiungimento della meta. Ogni teoria organica infatti ricapitola, e nello stesso tempo cancella, le frammentarie teorie precedenti: risulta evidente ciò che si guadagna in termini di efficienza e rapidità, meno chiaro è ciò che si perde (Lakatos, 1976). Ora accade che l'enunciazione di una teoria nella sua forma compiuta, piuttosto che attrarre ed affascinare per la sua rigorosa bellezza ed eleganza, susciti sensazioni sgradevoli, noia e rifiuto.
A questa riflessione segue quella che alcuni famosi e creativi matematici, che hanno lasciato traccia delle modalità con cui sono pervenuti alle loro scoperte, descrivono intuizioni ed emozioni affini alle esperienze artistiche o "estatiche" e percorsi che ben poco hanno a che fare con gli eleganti e stringati ragionamenti logici proposti agli studenti.
E' forse sull'intuizione di queste determinanti dell'animo umano, e più specificatamente infantile ed adolescenziale, che da molti anni, in Italia e all' estero, si sono sviluppati programmi e progetti-pilota per l'insegnamento della matematica. Dal momento che gran parte del lavoro didattico svolto è stato esposto in pubbliche mostre, è stato anche possibile vedere come il linguaggio matematico possa costituire una particolare griglia di lettura di opere tratte dal campo delle arti figurative. Possiamo allora ipotizzare che l'emozione estetica proveniente dall'opera d'arte sia in qualche modo legata anche all'emozione estetica proveniente dall'eleganza della teoria matematica che, in modo inconsapevole all'autore stesso, vi soggiace. C'è da pensare che l'arte costituisca un tramite facilitante, nel senso che stiamo indagando, all'apprendimento della matematica. Sarebbe naturalmente irrealistico delegare al miglioramento del metodo didattico la scomparsa delle difficoltà riscontrate, anche se sono possibili evidenti cambiamenti, in quanto le cause dei disturbi del pensiero descritti vanno comunque ricercate nell'ambito delle modalità con cui si è fondata e sviluppata la relazione primaria madre-bambino, per rimanere, s'intende, nell'ambito della teoresi psicoanalitica.
Non mancano autori e scuole di pensiero che partendo da presupposti completamente diversi hanno elaborato modelli e teorie che per taluni aspetti sono pervenute ad osservazioni e concettualizzazioni affini a quelle elaborate nell'ambito della psicoanalisi. Con quest'ultima la scuola cognitivista mostra una certa sintonia per quanto riguarda la concettualizzazione della difesa e dei meccanismi attraverso i quali essa si attua. In questo campo la convergenza delle ricerche acquista particolare significato per il nostro tema, poiché in esso occupa un posto di rilievo la difesa dallo stimolo penoso. Se accettiamo di concepire il soggetto come un complesso sistema di elaborazione dell'informazione, senza produrre in quest'occasione ulteriori specificazioni caratterizzanti, è facile riconoscere che esso può andare incontro a "disfunzioni dell'elaborazione". Queste disfunzioni possono consistere in un'elaborazione mancata o scorretta. Le cause di queste disfunzioni possono essere identificate, in questo schema, con desideri o paure che spingono il soggetto ad evitare certe elaborazioni o a realizzarle inadeguatamente. Anche se la ricerca nel settore specifico del trattamento delle emozioni non consente ancora di effettuare delle sintesi affrettate, sembra indubbio che la connotazione emotiva degli input è intimamente legata ai disturbi di elaborazione. L' evitamento cognitivo è da mettere in rapporto con i fenomeni di generalizzazione retroattiva che spiegano sia la perdita di consapevolezza del materiale evitato e del processo di evitamento che le caratteristiche peculiari (psicoanaliticamente si direbbe di processo primario) che acquista il processo stesso di elaborazione (cfr. M.H. Erdelyi, 1985). Il risultato dell'evitamento viene percepito in termini di deficit più o meno gravi delle funzioni cognitive.
Questo modello consente inoltre di prendere in considerazione, attraverso le nozioni di difesa e di vigilanza percettiva, noti concetti della psicoanalisi freudiana (come il ritiro degli investimenti di attenzione) che si rivelano nodali nella teorizzazione dei meccanismi attraverso i quali si attua la difesa. Sono fenomeni che possono essere efficacemente simulati al calcolatore.
Sembra indubbio che un modello di questo tipo offra, a chi cerca di mettere in rapporto le ricerche cognitive con quelle psicoanalitiche (come ad esempio Erdelyi), la possibilità di unificare i fenomeni dinamici in un sistema teorico formalizzato. E' altrettanto evidente che ogni sistema di questa natura lascia irrisolte due questioni che sono essenziali nella concezione psicoanalitica dei meccanismi di difesa. E cioè: la varietà e specificità dei diversi meccanismi e i loro valori semantici.
Così pure vorremmo ricordare l'opera di Jean Piaget, che dalla sua tesi di laurea in zoologia (1917) alla sua morte (1980) lavorò senza sosta nella costruzione di un disegno coerente di epistemologia genetica. Benché controverso e per alcuni versi forse superato, il suo contributo alla comprensione dello sviluppo cognitivo e, nel nostro caso particolare, dello sviluppo del pensiero ipotetico-deduttivo e formale dall'infanzia all'adolescenza, è di grande importanza.
La specificità del libro, per quanto riguarda il nostro argomento, va letta nelle conclusioni a cui arrivano gli autori, prima attraverso lo sviluppo delle rispettive competenze, poi nella confluenza delle loro vedute, secondo le quali i problemi posti dalla formalizzazione possono avere una qualche corrispondenza coi meccanismi mentali correnti. Piaget sottolinea che si potrebbe anche concludere che questi meccanismi correlativi alla formalizzazione si attualizzano solo in un'élite di soggetti (matematici e logici) e ciononostante sostenere l'esistenza delle strutture logico-matematiche come patrimonio di ogni soggetto. L'attualizzazione di queste strutture, nelle sue più spinte manifestazioni verso la formalizzazione, rappresenterebbe un punto alto, e non tanto comune, delle realizzazioni delle potenzialità umane.
Il matematico e il logico quindi "riscopriranno le strutture che agivano già nel pensiero pre-scientifico e costruiranno la teoria corrispondente", ciò è valido anche per le più spinte formalizzazioni. Si veda in proposito il fresco, intuitivo e disordinato, ma fertile, scritto di S. Ferenczi, Matematica (1920 circa). Ci sembra interessante accostare il concetto appena esposto al punto di vista della Milner per quanto riguarda le modalità con cui il bambino sviluppa la sua potenzialità cognitiva e simbolica passando da uno stadio al successivo. Entrambe le concezioni sembrano presupporre una potenzialità innata che per essere completamente sviluppata nel pensiero logico-formale ha bisogno di un humus contestuale, che per la Milner è rappresentato dallo spazio del gioco, senza il quale non ha la possibilità di attualizzarsi e rimane inespressa. Bibliografia Beth E.W. e Piaget J., (1961), Epistémologie mathématique et psychologie. Essai sur les relations entre la logique formelle ei la -pensée réelle, Paris, P.U.F. Bernardini C., (1989), Il piacere della razionalità, "L'Educatore", 6, 1989. Bion W.R., (1 962a), Una teoria del pensiero, in Analisi degli schizofrenici e pensiero Psicoanalitico, Roma, A. Armando, 1979. Bion W.R., (1962b), Apprendere dall'esperienza, Roma, A. Armando, 1979. Bion W.R., (1 963.), Gli elementi della psicoanalisi, Roma, A. Armando, 1973. Bion W.R., (1 976), Intervista, in Il cambiamento catastrofico, Torino, Loescher, 1981. Bourbaki N., (1969), Eléments d' histoire des mathématiques. DSM III R.; manuale diagnostico e statistico dei disturbi mentali, a cura di: Andreoli V., Cassano G., Ross R., Paris, Masson, 1989. Erdelyi M.H., (1 985), Freud cognitivista, Bologna, Il Mulino, 1988. Ferenczi S., (1920 circa), Matematica, In Fondamenti di psicoanalisi, voi. IV, Rimini, Guaraldi, 1974. Fine R. e Fine B., (1977), The matematician as a healty narcissist, in The narcissist condition, cap, 9, Human Science Press. Freud S., (1 895), Progetto di una psicologia, OSF, vol. II, Torino, Boringhieri, 1978. Freud S., (1 91 1), Precisazioni sui due principi dell'accadere psichico, in OSF, vol. VI, Torino, Boringhieri, 1978. Freud S., (1925a), La negazione, in OSF, vol. X, Torino, Boringhieri, 1978. Freud S., (1 925b), Inibizione, sintomo, angoscia, in OSF, voi. X, Torino, Boringhieri, 1978. Johnson-Laird P., (1 983), Mental models, Carnbridge, Harvard University Press. Klein M., (1923), La scuola nello sviluppo libidico del bambino, In Scritti 1921-1958, Torino Boringhieri, 1978. Klein M., (1931), Contributo alla teoria dell'inibizione intellettiva, in Scritti 1921-1958, Torino, Boringhieri, 1978. Lakatos I., (1 976), Dimostrazioni e confutazioni. la logica della scoperta matematica, Milano, Feltrinclli, 1979. Lolli G., (1988), Capire una dimostrazione, Bologna, Il Mulino. Meltzer D., (1975), Esplorazioi sull'autismo, Torino, Boringhieri, 1977. Milner M., (1 955), Il ruolo della Illusione nella formazione del simbolo, in Nuove vie della psicoanalisi, Milano, Il Saggiatore, 1966, Paulos J.A., (1 988), Innumeracy. Mathematical illiteracy and its consequence.s, New York, Hin and Wane. Rosen V.H., (1953), On mathematical illumination and the mathematical though process, "Psychoanalitic Study of the child", 8,1953. Segal H., (1957), Note sulla formazione del simbolo, in Scritti psicoanalitici, Roma, Astrolabio, 1984.
|